Hi, I'm Walter.
What I'm working on
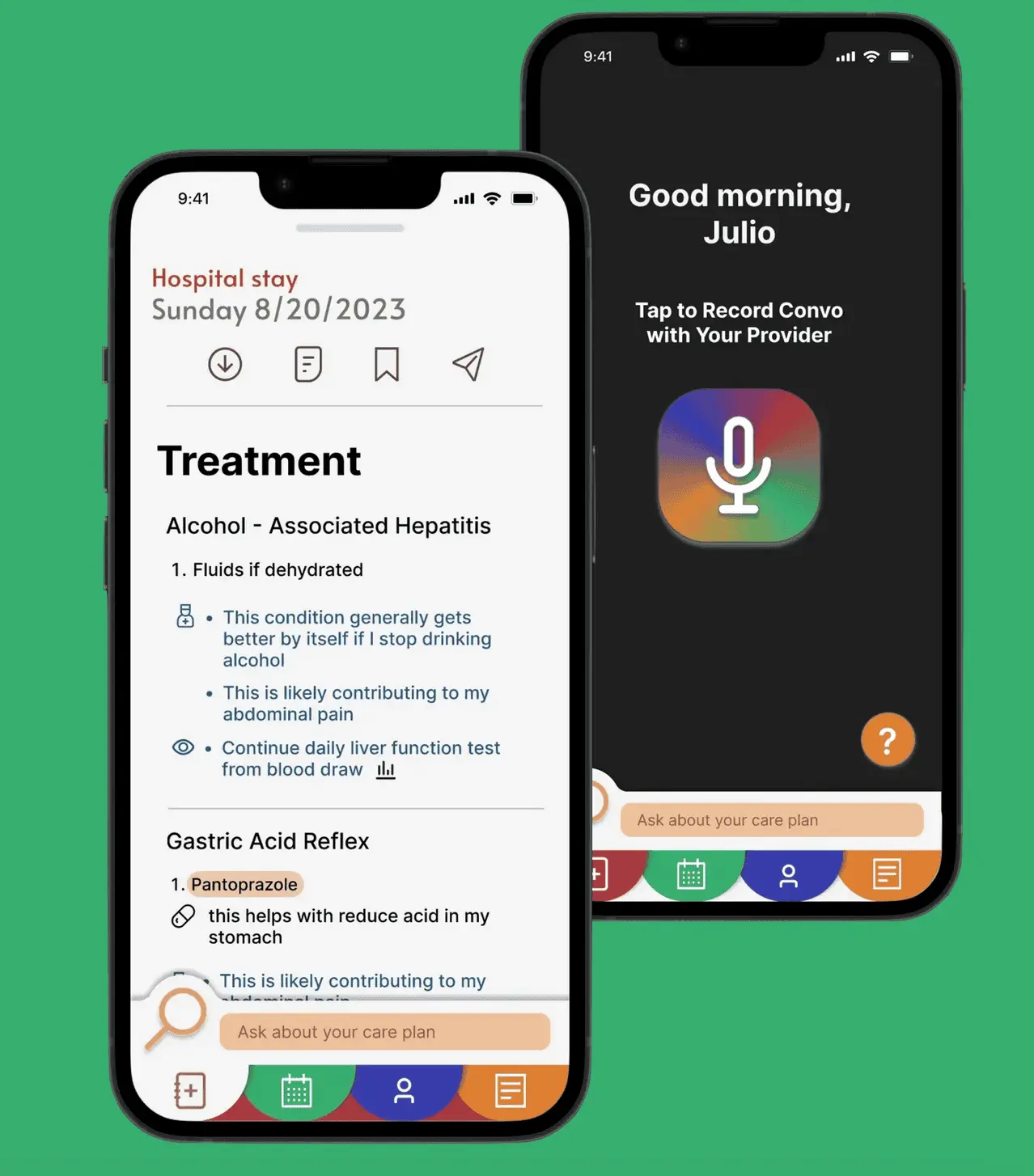
I'm helping readers read better in the age of AI with an app called BookSlice.
The decline is already happening. Today, people read fewer books than before, English majors can't read, and people are overreliant on large language models.
Things will get much worse, and my goal is to help as many of us use these tools to read better, not worse.
0-to-1 product development
I do 0-to-1 product development for startups and solo entrepreneurs. Book a free discovery call if you'd like to speedrun your business launch.

About
I'm on a career break to work on my own projects. To be honest, it's a bit ironic to call it a "break" since what I've really been doing is work days, nights, and weekends. Incredibly fulfilling though.
Last year (2024), I learnt how to code and built several apps. BookSlice was my most profitable app—it was supported by Microsoft for Startups, featured in The Straits Times, and placed 2nd on ProductHunt. I also built Malaysia's #1 website for Pengajian Am (ranked #1 on Google), and a travel visa app that was featured on Mint, India's #1 finance news site.
From 2020 to 2023, I worked as a Product Manager at igloohome, leading teams of engineers and designers (30+ persons) on all things consumer. We launched about 15 different software and hardware products while I was there.
My formal education is in mechanical engineering at NUS and liberal arts at USP.
For projects and consulting inquiries, feel free to email me or book a discovery call.